Свойства отношений на множестве. Бинарные отношения

Бинарные отношения и их свойства. Специальные бинарные отношения.

Бинарным отношением на множестве А называется подмножество его квадрата RÍ A 2 . Бинарным отношением между множествами А и В называются подмножество принадлежащее декартовому произведению 2-х множеств: RÍ АхВ.

Если упорядоченная пара (а1, а2) принадлежит отношению R, то говорят что а1 R а2, то есть между элементом а1 и а2 уст-но отношение R.

Областью определения бинарного отношения называется множество элементов а, в котором в принадлежит бинарному отношению: þ_R=.

Областью значения бинарного отношения называют множество b, в котором а принадлежит бинарному значению:

Обратное отношение для отношения R называется отношение : R -1 =<(b,a)|(a,b) Î R >.

Отношение можно задать:

– с помощью любого способа задания множеств

– С помощью матрицы бинарного отношения. Матрица бинарного отношения это квадратная матрица R элементы которой определяются следующим образом rij=1, (ai,aj)Î R, 0 – в противном случае.

– С использованием графа. Каждому бинарному отношению можно подставить в соответствие граф G(X,U), содержащий множество вершин Х, и множество ребер U. При этом вершины aj ai соединяются дугой если упорядоченная пара aj ai Î R. Так как отношения являются множеством упорядоченных пар, то для отношения можно определить те же операции , что и для множеств (объединение, пересечение, разность, дополнение, симметрическая разность).

Свойство бинарных отношений:

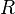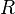1) Рефлексивность. Пусть на множестве А задано бинарное отношение R. Бинарное отношение называется рефлексивным, если для любого элемента А упорядоченная пара из этого элемента принадлежит R: для любого A(a,a) Î R. Т.е. бинарное отношение на множестве называется рефлексивным, если всякий элемент этого множества находится в отношении с самим собой.

Матрица рефлексивного отношения на диагонали содержит 1, а граф бинарного отношения имеет петли.

2)Антирефлексивность. Бинарные отношения являются антирефлексивными, если: для любого A(a,a) Ï R.

Матрица антирефлексивного отношения на диагонали содержит 0, а граф не имеет петель.

3)Симметричность. Бинарное отношение 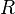на множестве X называется симметричным, если для каждой пары элементов множества выполнение отношения влечёт выполнение отношения . Отношение 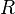симметрично, если .

Матрица симметричного бинарного отношения симметрична относительно главной диагонали. В графе все пары вершин соединены 2-мя противоположно направленными дугами.

4) Антисимметричночть. В математике бинарное отношение 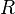на множестве X называется антисимметричным, если для каждой пары элементов множества выполнение отношений и влечёт , или, что то же самое, выполнение отношений и возможно только для равных и .

Матрица антисимметричного бинарного отношения не симметрична относительно главной диагонали, в графе отсутствуют противоположно направленные дуги.

5) Транзитивность. Бинарное отношение называют транзитивным, если :

В графе задающего транзитивное бинарное отношение для каждой пары дуг таких, что конец первой совпадает с началом второй, существует дуга, соединяющая начало первой дуги с концом второй.

Специальные бинарные отношения:

1) Отношение Эквивалентности на множестве А это отношение, обладающее свойством рефлекисвности, симметричности и транзитивности. (Отношение равенства, отношение параллельности).

2) Отношения строгого порядка: это бинарное отношение на множестве А, обладающее свойствами антирефлексивности, антисимметричности и транзитивности.

3) Отношения нестрого порядка- бинарные отношения, обладающие свойствами рефлексивности. Антисимметричности и транзитивности.

Бинарные отношения и их свойства

Основы дискретной математики.

Понятие множества. Отношение между множествами.

Множество – совокупность объектов, обладающих определенным свойством, объединенных в единое целое.

Объекты, составляющие множество называются элементами множества. Для того чтобы некоторую совокупность объектов можно было называть множеством должны выполняться следующие условия:

· Должно существовать правило, по которому моно определить принадлежит ли элемент к данной совокупности.

· Должно существовать правило, по которому элементы можно отличить друг от друга.

Множества обозначаются заглавными буквами, а его элементы маленькими. Способы задания множеств:

· Перечисление элементов множества. – для конечных множеств.

· Указание характеристического свойства .

Пустым множеством – называется множество, не содержащее ни одного элемента (Ø).

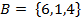
Два множества называются равными, если они состоят из одних и тех же элементов. , A=B

Множество B называется подмножеством множества А ( , тогда и только тогда когда все элементы множества B принадлежат множеству A.

Например: , B =>

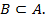
Свойство:

Примечание: обычно рассматривают подмножество одного и того е множества, которое называется универсальным (u). Универсальное множество содержит все элементы.

Операции над множествами.

Н-р: , ,

2.Пересечением 2-х множеств называется новое множество, состоящее из элементов, одновременно принадлежат и первому и второму множеству.

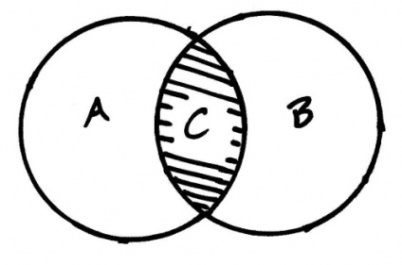
Н-р: , ,

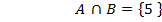
Свойство: операции объединения и пересечения.

· Коммутативность.

;

· Ассоциативность. ;

;

· Дистрибутивный. ;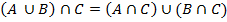

;

Свойства бинарных отношений (стр. 1 из 4)

2. Слабая рефлексивность:

3. Сильная рефлексивность:

5. Слабая антирефлексивность:

6. Сильная антирефлексивность:

10. Сильная линейность:

11. Слабая линейность:

Рефлексивность, свойство бинарных (двуместных, двучленных) отношений, выражающее выполнимость их для пар объектов с совпадающими членами (так сказать, между объектом и его “зеркальным отражением”): отношение R называется рефлексивным, если для любого объекта х из области его определения выполняется xRx. Типичные и наиболее важные примеры рефлексивных отношений: отношения типа равенства (тождества, эквивалентности, подобия и т.п.: любой предмет равен самому себе) и отношения нестрогого порядка (любой предмет не меньше и не больше самого себя). Интуитивные представления о “равенстве” (эквивалентности, подобии и т.п.), очевидным образом наделяющие его свойствами симметричности и транзитивности, “вынуждают” и свойство Р., поскольку последнее свойство следует из первых двух. Поэтому многие употребительные в математике отношения, по определению Р. не обладающие, оказывается естественным доопределить таким образом, чтобы они становились рефлексивными, например, считать, что каждая прямая или плоскость параллельна самой себе, и т.п.

Глава 1. Элементы теории множеств

1.1 Множества

Наиболее простая структура данных, используемая в математике, имеет место в случае, когда между отдельными изолированными данными отсутствуют какие-либо взаимосвязи. Совокупность таких данных представляет собой множество . Понятие множества является неопределяемым понятием. Множество не обладает внутренней структурой. Множество можно представить себе как совокупность элементов, обладающих некоторым общим свойством. Для того чтобы некоторую совокупность элементов можно было назвать множеством, необходимо, чтобы выполнялись следующие условия:

Должно существовать правило, позволяющее определить, принадлежит ли указанный элемент данной совокупности.

Должно существовать правило, позволяющее отличать элементы друг от друга. (Это, в частности, означает, что множество не может содержать двух одинаковых элементов).

Множества обычно обозначаются заглавными латинскими буквами. Если элемент

Если каждый элемент множества

Используя понятие множества можно построить более сложные и содержательные объекты.

1.2 Операции над множествами

Основными операциями над множествами являются объединение , пересечение и разность .

Определение 1 . Объединением двух множеств называется новое множество

Определение 2 . Пересечением двух множеств называется новое множество

Определение 3 . Разностью двух множеств называется новое множество

Если класс объектов, на которых определяются различные множества обозначить

1.3 Декартово произведение множеств

Одним из способов конструирования новых объектов из уже имеющихся множеств является декартово произведение множеств .

Определение 4 . Декартовым (прямым) произведением множеств

Определение 5 . Степенью декартового произведения

Замечание. Если все множества

1.4 Отношение

Определение 6 . Подмножество

Определение 7 . Мощность множества кортежей, входящих в отношение

Замечание. Понятие отношения является очень важным не только с математической точки зрения. Понятие отношения фактически лежит в основе всей реляционной теории баз данных. Как будет показано ниже, отношения являются математическим аналогом таблиц . Сам термин “реляционное представление данных”, впервые введенный Коддом [43], происходит от термина relation , понимаемом именно в смысле этого определения.

Т. к. любое множество можно рассматривать как декартовое произведение степени 1, то любое подмножество, как и любое множество, можно считать отношением степени 1. Это не очень интересный пример, свидетельствующий лишь о том, что термины “отношение степени 1” и “подмножество” являются синонимами. Нетривиальность понятия отношения проявляется, когда степень отношения больше 1. Ключевыми здесь являются два момента:

Во-первых , все элементы отношения есть однотипные кортежи. Однотипность кортежей позволяет считать их аналогами строк в простой таблице, т.е. в такой таблице, в которой все строки состоят из одинакового числа ячеек и в соответствующих ячейках содержатся одинаковые типы данных. Например, отношение, состоящее из трех следующих кортежей < (1, "Иванов", 1000), (2, "Петров", 2000), (3, "Сидоров", 3000) >можно считать таблицей, содержащей данные о сотрудниках и их зарплатах. Такая таблица будет иметь три строки и три колонки, причем в каждой колонке содержатся данные одного типа.

В противоположность этому рассмотрим множество < (1), (1,2), (1, 2,3) >, состоящее из разнотипных числовых кортежей. Это множество не является отношением ни в

Источники:

http://studopedia.ru/19_398701_binarnie-otnosheniya-i-ih-svoystva-spetsialnie-binarnie-otnosheniya.html
http://megaobuchalka.ru/7/29655.html
http://mirznanii.com/a/313782/svoystva-binarnykh-otnosheniy